Working with Missing Data

Libraries

import pandas as pd
# to display all columns
pd.set_option('display.max.columns', None)
# to display the entire contents of a cell
pd.set_option('display.max_colwidth', None)
import numpy as np

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.style.use("ggplot")

mvc = pd.read_csv("../datasets/nypd_mvc_2018.csv")
mvc.head()

	unique_key	date	time	borough	location	on_street	cross_street	off_street	pedestrians_injured	cyclist_injured	motorist_injured	total_injured	pedestrians_killed	cyclist_killed	motorist_killed	total_killed	vehicle_1	vehicle_2	vehicle_3	vehicle_4	vehicle_5	cause_vehicle_1	cause_vehicle_2	cause_vehicle_3	cause_vehicle_4	cause_vehicle_5
0	3869058	2018-03-23	21:40	MANHATTAN	(40.742832, -74.00771)	WEST 15 STREET	10 AVENUE	NaN	0	0	0	0.0	0	0	0	0.0	PASSENGER VEHICLE	NaN	NaN	NaN	NaN	Following Too Closely	Unspecified	NaN	NaN	NaN
1	3847947	2018-02-13	14:45	BROOKLYN	(40.623714, -73.99314)	16 AVENUE	62 STREET	NaN	0	0	0	0.0	0	0	0	0.0	SPORT UTILITY / STATION WAGON	DS	NaN	NaN	NaN	Backing Unsafely	Unspecified	NaN	NaN	NaN
2	3914294	2018-06-04	0:00	NaN	(40.591755, -73.9083)	BELT PARKWAY	NaN	NaN	0	0	1	1.0	0	0	0	0.0	Station Wagon/Sport Utility Vehicle	Sedan	NaN	NaN	NaN	Following Too Closely	Unspecified	NaN	NaN	NaN
3	3915069	2018-06-05	6:36	QUEENS	(40.73602, -73.87954)	GRAND AVENUE	VANLOON STREET	NaN	0	0	0	0.0	0	0	0	0.0	Sedan	Sedan	NaN	NaN	NaN	Glare	Passing Too Closely	NaN	NaN	NaN
4	3923123	2018-06-16	15:45	BRONX	(40.884727, -73.89945)	NaN	NaN	208 WEST 238 STREET	0	0	0	0.0	0	0	0	0.0	Station Wagon/Sport Utility Vehicle	Sedan	NaN	NaN	NaN	Turning Improperly	Unspecified	NaN	NaN	NaN

A summary of the columns and their data is below:

• unique_key: A unique identifier for each collision.
• date, time: Date and time of the collision.
• borough: The borough, or area of New York City, where the collision occurred.
• location: Latitude and longitude coordinates for the collision.
• on_street, cross_street, off_street: Details of the street or intersection where the collision occurred.
• pedestrians_injured: Number of pedestrians who were injured.
• cyclist_injured: Number of people traveling on a bicycle who were injured.
• motorist_injured: Number of people traveling in a vehicle who were injured.
• total_injured: Total number of people injured.
• pedestrians_killed: Number of pedestrians who were killed.
• cyclist_killed: Number of people traveling on a bicycle who were killed.
• motorist_killed: Number of people traveling in a vehicle who were killed.
• total_killed: Total number of people killed.
• vehicle_1 through vehicle_5: Type of each vehicle involved in the accident.
• cause_vehicle_1 through cause_vehicle_5: Contributing factor for each vehicle in the accident.

Missing Values

mvc.isna().sum()

unique_key                 0
date                       0
time                       0
borough                20646
location                3885
on_street              13961
cross_street           29249
off_street             44093
pedestrians_injured        0
cyclist_injured            0
motorist_injured           0
total_injured              1
pedestrians_killed         0
cyclist_killed             0
motorist_killed            0
total_killed               5
vehicle_1                355
vehicle_2              12262
vehicle_3              54352
vehicle_4              57158
vehicle_5              57681
cause_vehicle_1          175
cause_vehicle_2         8692
cause_vehicle_3        54134
cause_vehicle_4        57111
cause_vehicle_5        57671
dtype: int64

To give us a better picture of the null values in the data, let’s calculate the percentage of null values in each column.

null_df = pd.DataFrame({'null_counts':mvc.isna().sum(), 'null_pct':mvc.isna().sum()/mvc.shape[0] * 100}).T.astype(int).T
null_df

	null_counts	null_pct
unique_key	0	0
date	0	0
time	0	0
borough	20646	35
location	3885	6
on_street	13961	24
cross_street	29249	50
off_street	44093	76
pedestrians_injured	0	0
cyclist_injured	0	0
motorist_injured	0	0
total_injured	1	0
pedestrians_killed	0	0
cyclist_killed	0	0
motorist_killed	0	0
total_killed	5	0
vehicle_1	355	0
vehicle_2	12262	21
vehicle_3	54352	93
vehicle_4	57158	98
vehicle_5	57681	99
cause_vehicle_1	175	0
cause_vehicle_2	8692	15
cause_vehicle_3	54134	93
cause_vehicle_4	57111	98
cause_vehicle_5	57671	99

About a third of the columns have no null values, with the rest ranging from less than 1% to 99%! To make things easier, let’s start by looking at the group of columns that relate to people killed in collisions.

null_df.loc[[column for column in mvc.columns if "killed" in column]]

	null_counts	null_pct
pedestrians_killed	0	0
cyclist_killed	0	0
motorist_killed	0	0
total_killed	5	0

We can see that each of the individual categories have no missing values, but the total_killed column has five missing values.

If you think about it, the total number of people killed should be the sum of each of the individual categories. We might be able to “fill in” the missing values with the sums of the individual columns for that row.

Important

The technical name for filling in a missing value with a replacement value is called imputation.

Verifying the total columns

killed = mvc[[col for col in mvc.columns if 'killed' in col]].copy()
killed_manual_sum = killed.iloc[:, :3].sum(axis="columns")
killed_mask = killed_manual_sum != killed.total_killed
killed_non_eq = killed[killed_mask]
killed_non_eq

	pedestrians_killed	cyclist_killed	motorist_killed	total_killed
3508	0	0	0	NaN
20163	0	0	0	NaN
22046	0	0	1	0.0
48719	0	0	0	NaN
55148	0	0	0	NaN
55699	0	0	0	NaN

Filling and Verifying the killed and the injured data

The killed_non_eq dataframe has six rows. We can categorize these into two categories:

• Five rows where the total_killed is not equal to the sum of the other columns because the total value is missing.
• One row where the total_killed is less than the sum of the other columns.

From this, we can conclude that filling null values with the sum of the columns is a fairly good choice for our imputation, given that only six rows out of around 58,000 don’t match this pattern.

We’ve also identified a row that has suspicious data - one that doesn’t sum correctly. Once we have imputed values for all rows with missing values for total_killed, we’ll mark this suspect row by setting its value to NaN.

# fix the killed values
killed['total_killed'] = killed['total_killed'].mask(killed['total_killed'].isnull(), killed_manual_sum)
killed['total_killed'] = killed['total_killed'].mask(killed['total_killed'] != killed_manual_sum, np.nan)

# Create an injured dataframe and manually sum values
injured = mvc[[col for col in mvc.columns if 'injured' in col]].copy()
injured_manual_sum = injured.iloc[:,:3].sum(axis=1)

injured['total_injured'] = injured.total_injured.mask(injured.total_injured.isnull(), injured_manual_sum)

injured['total_injured'] = injured.total_injured.mask(injured.total_injured != injured_manual_sum, np.nan)

Let’s summarize the count of null values before and after our changes:

summary = {
    'injured': [
        mvc['total_injured'].isnull().sum(),
        injured['total_injured'].isnull().sum()
    ],
    'killed': [
        mvc['total_killed'].isnull().sum(),
        killed['total_killed'].isnull().sum()
    ]
}
pd.DataFrame(summary, index=['before','after'])

	injured	killed
before	1	5
after	21	1

For the total_killed column, the number of values has gone down from 5 to 1. For the total_injured column, the number of values has actually gone up — from 1 to 21. This might sound like we’ve done the opposite of what we set out to do, but what we’ve actually done is fill all the null values and identify values that have suspect data. This will make any analysis we do on this data more accurate in the long run.

Let’s assign the values from the killed and injured dataframe back to the main mvc dataframe:

mvc['total_injured']=injured.total_injured
mvc['total_killed']=killed.total_killed

Visualizing the missing data with plots

Earlier, we used a table of numbers to understand the number of missing values in our dataframe. A different approach we can take is to use a plot to visualize the missing values. The function below uses seaborn.heatmap() to represent null values as dark squares and non-null values as light squares:

def plot_null_matrix(df, figsize=(20,15)):
    """Plot null values as light squares and non-null values as dark squares"""
    plt.figure(figsize=figsize)
    df_null = df.isnull()
    sns.heatmap(~df_null, cbar=False, yticklabels=False)
    plt.xticks(rotation=90, size="x-large")
    plt.show()

Let’s look at how the function works by using it to plot just the first row of our mvc dataframe. We’ll display the first row as a table immediately below so it’s easy to compare:

plot_null_matrix(mvc.head(1), figsize=(20,2))

mvc.head(1)

	unique_key	date	time	borough	location	on_street	cross_street	off_street	pedestrians_injured	cyclist_injured	motorist_injured	total_injured	pedestrians_killed	cyclist_killed	motorist_killed	total_killed	vehicle_1	vehicle_2	vehicle_3	vehicle_4	vehicle_5	cause_vehicle_1	cause_vehicle_2	cause_vehicle_3	cause_vehicle_4	cause_vehicle_5
0	3869058	2018-03-23	21:40	MANHATTAN	(40.742832, -74.00771)	WEST 15 STREET	10 AVENUE	NaN	0	0	0	0.0	0	0	0	0.0	PASSENGER VEHICLE	NaN	NaN	NaN	NaN	Following Too Closely	Unspecified	NaN	NaN	NaN

Each value is represented by a light square, and each missing value is represented by a dark square.

Let’s look at what a plot matrix looks like for the whole dataframe:

plot_null_matrix(mvc)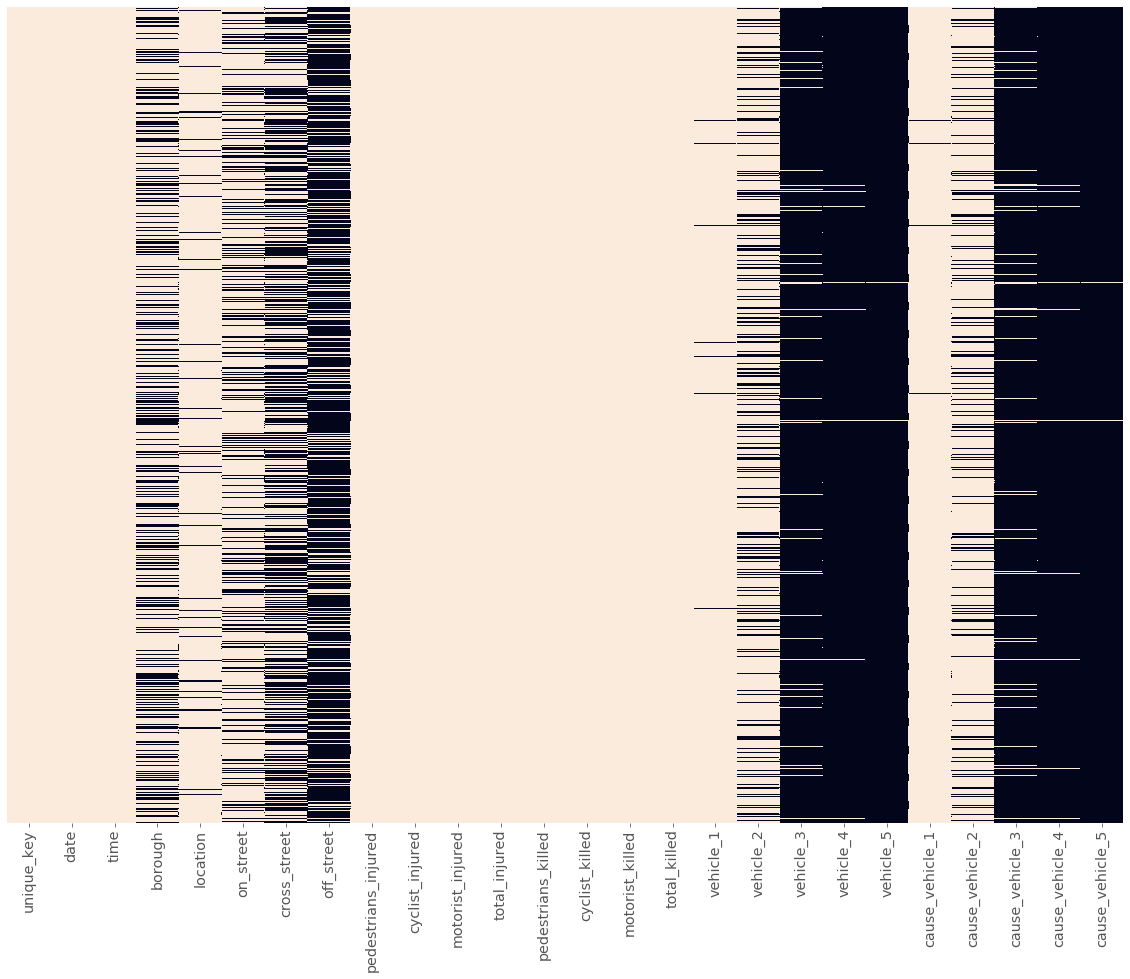

We can make some immediate interpretations about our dataframe:

• The first three columns have few to no missing values.
• The next five columns have missing values scattered throughout, with each column seeming to have its own density of missing values.
• The next eight columns are the injury and killed columns we just cleaned, and only have a few missing values.
• The last 10 columns seem to break into two groups of five, with each group of five having similar patterns of null/non-null values.

Let’s examine the pattern in the last 10 columns a little more closely. We can calculate the relationship between two sets of columns, known as correlation.

cols_with_missing_vals = mvc.columns[mvc.isnull().sum()>0]
missing_corr = mvc[cols_with_missing_vals].isnull().corr()
missing_corr

	borough	location	on_street	cross_street	off_street	total_injured	total_killed	vehicle_1	vehicle_2	vehicle_3	vehicle_4	vehicle_5	cause_vehicle_1	cause_vehicle_2	cause_vehicle_3	cause_vehicle_4	cause_vehicle_5
borough	1.000000	0.190105	-0.350190	0.409107	0.362189	-0.002827	0.005582	-0.018325	-0.077516	-0.061932	-0.020406	-0.010733	-0.012115	-0.058596	-0.060542	-0.020158	-0.011348
location	0.190105	1.000000	-0.073975	-0.069719	0.084579	-0.001486	0.015496	-0.010466	-0.033842	-0.000927	0.004655	-0.005797	-0.003458	-0.021373	0.000684	0.004604	-0.004841
on_street	-0.350190	-0.073975	1.000000	0.557767	-0.991030	0.006220	-0.002344	-0.001889	0.119647	0.020867	0.004172	-0.002768	0.001307	0.087374	0.017426	0.002737	-0.003107
cross_street	0.409107	-0.069719	0.557767	1.000000	-0.552763	0.002513	0.004112	-0.017018	0.043799	-0.049910	-0.021137	-0.012003	-0.009102	0.031189	-0.052159	-0.022074	-0.013455
off_street	0.362189	0.084579	-0.991030	-0.552763	1.000000	-0.004266	0.002323	0.001812	-0.121129	-0.022404	-0.004074	0.002492	-0.001738	-0.088187	-0.019120	-0.002580	0.002863
total_injured	-0.002827	-0.001486	0.006220	0.002513	-0.004266	1.000000	-0.000079	0.079840	0.025644	-0.002757	0.002118	0.001073	0.131140	0.030082	-0.002388	0.002188	0.001102
total_killed	0.005582	0.015496	-0.002344	0.004112	0.002323	-0.000079	1.000000	-0.000327	0.008017	0.001057	0.000462	0.000234	-0.000229	0.009888	0.001091	0.000477	0.000240
vehicle_1	-0.018325	-0.010466	-0.001889	-0.017018	0.001812	0.079840	-0.000327	1.000000	0.151516	0.019972	0.008732	0.004425	0.604281	0.180678	0.020624	0.009022	0.004545
vehicle_2	-0.077516	-0.033842	0.119647	0.043799	-0.121129	0.025644	0.008017	0.151516	1.000000	0.131813	0.057631	0.029208	0.106214	0.784402	0.132499	0.058050	0.029264
vehicle_3	-0.061932	-0.000927	0.020867	-0.049910	-0.022404	-0.002757	0.001057	0.019972	0.131813	1.000000	0.437214	0.221585	0.014000	0.106874	0.961316	0.448525	0.225067
vehicle_4	-0.020406	0.004655	0.004172	-0.021137	-0.004074	0.002118	0.000462	0.008732	0.057631	0.437214	1.000000	0.506810	0.006121	0.046727	0.423394	0.963723	0.515058
vehicle_5	-0.010733	-0.005797	-0.002768	-0.012003	0.002492	0.001073	0.000234	0.004425	0.029208	0.221585	0.506810	1.000000	0.003102	0.023682	0.214580	0.490537	0.973664
cause_vehicle_1	-0.012115	-0.003458	0.001307	-0.009102	-0.001738	0.131140	-0.000229	0.604281	0.106214	0.014000	0.006121	0.003102	1.000000	0.131000	0.014457	0.006324	0.003186
cause_vehicle_2	-0.058596	-0.021373	0.087374	0.031189	-0.088187	0.030082	0.009888	0.180678	0.784402	0.106874	0.046727	0.023682	0.131000	1.000000	0.110362	0.048277	0.024322
cause_vehicle_3	-0.060542	0.000684	0.017426	-0.052159	-0.019120	-0.002388	0.001091	0.020624	0.132499	0.961316	0.423394	0.214580	0.014457	0.110362	1.000000	0.437440	0.220384
cause_vehicle_4	-0.020158	0.004604	0.002737	-0.022074	-0.002580	0.002188	0.000477	0.009022	0.058050	0.448525	0.963723	0.490537	0.006324	0.048277	0.437440	1.000000	0.503805
cause_vehicle_5	-0.011348	-0.004841	-0.003107	-0.013455	0.002863	0.001102	0.000240	0.004545	0.029264	0.225067	0.515058	0.973664	0.003186	0.024322	0.220384	0.503805	1.000000

Each value is between -1 and 1, and represents the relationship between two columns. A number close to 1 or -1 represents a strong relationship, where a number in the middle (close to 0) represents a weak relationship.

If you look closely, you can see a diagonal line of 1s going from top left to bottom right. These values represent each columns relationship with itself, which of course is a perfect relationship. The values on the top/right of this “line of 1s” mirror the values on the bottom/left of this line: The table actually repeats every value twice!

Let’s create a correlation plot of just those last 10 columns to see if we can more closely identify the pattern we saw earlier in the matrix plot.

def plot_null_correlations(df):
    """create a correlation matrix only for columns with at least one missing value"""
    cols_with_missing_vals = df.columns[df.isnull().sum() > 0]
    missing_corr = df[cols_with_missing_vals].isnull().corr()
    
    # create a mask to avoid repeated values and make
    # the plot easier to read
    missing_corr = missing_corr.iloc[1:, :-1]
   
    mask = np.triu(np.ones_like(missing_corr), k=1)
    
    # plot a heatmap of the values
    plt.figure(figsize=(20,14))
    ax = sns.heatmap(missing_corr, vmin=-1, vmax=1, cbar=False,
                     cmap='RdBu', mask=mask, annot=True)
    
    # format the text in the plot to make it easier to read
    for text in ax.texts:
        t = float(text.get_text())
        if -0.05 < t < 0.01:
            text.set_text('')
        else:
            text.set_text(round(t, 2))
        text.set_fontsize('x-large')
    plt.xticks(rotation=90, size='x-large')
    plt.yticks(rotation=0, size='x-large')

    plt.show()

plot_null_correlations(mvc[[column for column in mvc.columns if 'vehicle' in column]])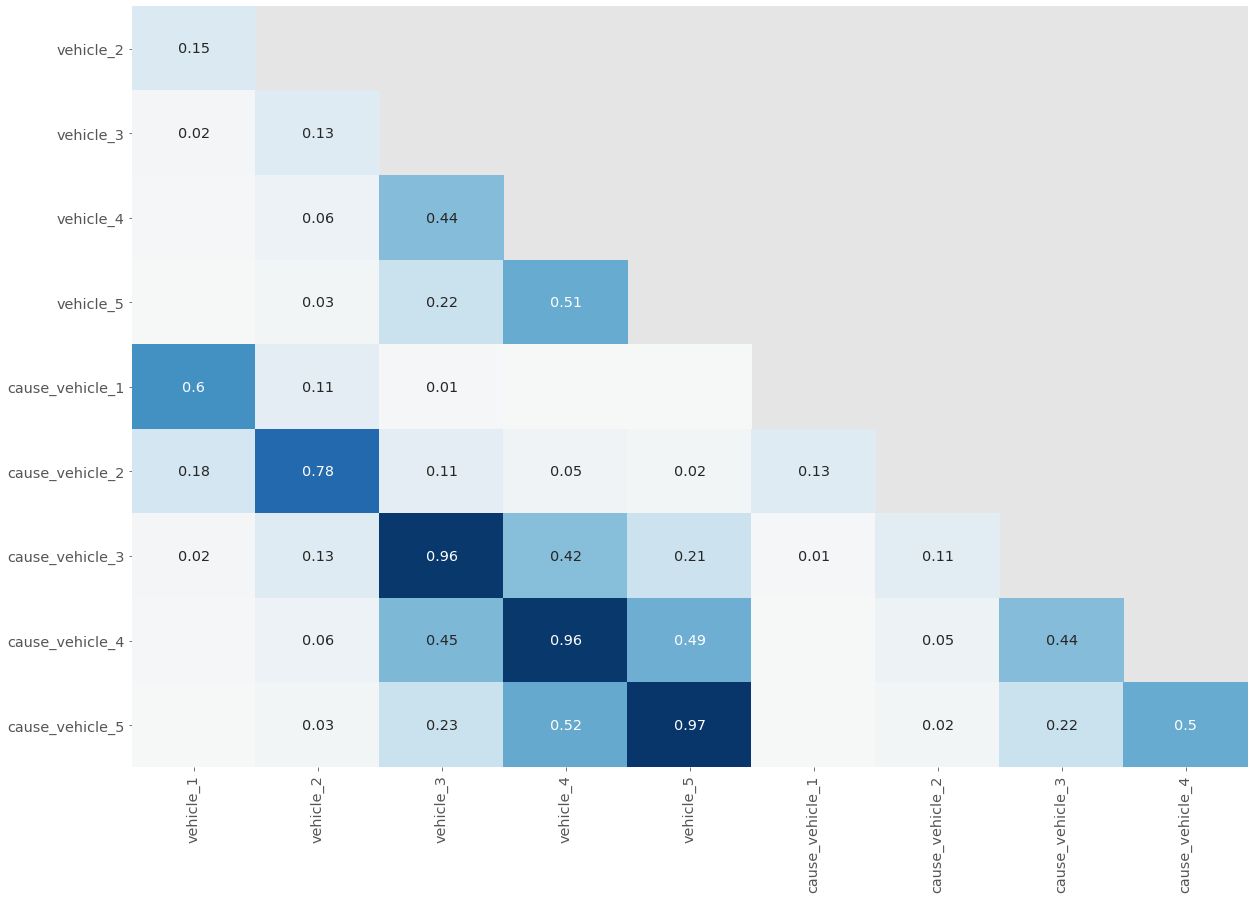

In our correlation plot:

• The “line of 1s” and the repeated values are removed so that it’s not visually overwhelming.
• Values very close to 0, where there is little to no relationship, aren’t labeled.
• Values close to 1 are dark blue and values close to -1 are light blue — the depth of color represents the strength of the relationship.

Analyzing Correlation in Missing Values

When a vehicle is in an accident, there is likely to be a cause, and vice-versa.

Let’s explore the variations in missing values from these five pairs of columns. We’ll create a dataframe that counts, for each pair:

• The number of values where the vehicle is missing when the cause is not missing.
• The number of values where the cause is missing when the vehicle is not missing.

col_labels = ['v_number', 'vehicle_missing', 'cause_missing']

vc_null_data = []

for v in range(1,6):
    v_col = 'vehicle_{}'.format(v)
    c_col = 'cause_vehicle_{}'.format(v)
    v_null = mvc[mvc[v_col].isnull() & mvc[c_col].notnull()].shape[0]
    c_null = mvc[mvc[v_col].notnull() & mvc[c_col].isnull()].shape[0]
    vc_null_data.append([v, v_null, c_null])
    
vc_null_df = pd.DataFrame(vc_null_data, columns=col_labels)
vc_null_df

	v_number	vehicle_missing	cause_missing
0	1	204	24
1	2	3793	223
2	3	242	24
3	4	50	3
4	5	10	0

Finding The Most Common Value Across multiple Columns

The analysis we indicates that there are roughly 4,500 missing values across the 10 columns. The easiest option for handling these would be to drop the rows with missing values. This would mean losing almost 10% of the total data, which is something we ideally want to avoid.

A better option is to impute the data, like we did earlier. Because the data in these columns is text data, we can’t perform a numeric calculation to impute missing data.

One common option when imputing is to use the most common value to fill in data. Let’s look at the common values across these columns and see if we can use that to make a decision.

Let’s count the most common values for the cause set of columns. We’ll start by selecting only the columns containing the substring cause.

cause = mvc[[c for c in mvc.columns if "cause_" in c]]
cause.head()

	cause_vehicle_1	cause_vehicle_2	cause_vehicle_3	cause_vehicle_4	cause_vehicle_5
0	Following Too Closely	Unspecified	NaN	NaN	NaN
1	Backing Unsafely	Unspecified	NaN	NaN	NaN
2	Following Too Closely	Unspecified	NaN	NaN	NaN
3	Glare	Passing Too Closely	NaN	NaN	NaN
4	Turning Improperly	Unspecified	NaN	NaN	NaN

Next, we’ll stack the values into a single series object:

cause_1d = cause.stack()
cause_1d.head()

0  cause_vehicle_1    Following Too Closely
   cause_vehicle_2              Unspecified
1  cause_vehicle_1         Backing Unsafely
   cause_vehicle_2              Unspecified
2  cause_vehicle_1    Following Too Closely
dtype: object

You may notice that the stacked version omits null values - this is fine, as we’re just interested in the most common non-null values.

Finally, we count the values in the series:

cause_counts = cause_1d.value_counts()
top10_causes = cause_counts.head(10)
top10_causes

Unspecified                       57481
Driver Inattention/Distraction    17650
Following Too Closely              6567
Failure to Yield Right-of-Way      4566
Passing or Lane Usage Improper     3260
Passing Too Closely                3045
Backing Unsafely                   3001
Other Vehicular                    2523
Unsafe Lane Changing               2372
Turning Improperly                 1590
dtype: int64

The most common non-null value for the cause columns is Unspecified, which presumably indicates that the officer reporting the collision was unable to determine the cause for that vehicle.

Let’s identify the most common non-null value for the vehicle columns.

v_cols = [c for c in mvc.columns if c.startswith("vehicle")]
top10_vehicles = mvc[v_cols].stack().value_counts().head(10)
top10_vehicles

Sedan                                  33133
Station Wagon/Sport Utility Vehicle    26124
PASSENGER VEHICLE                      16026
SPORT UTILITY / STATION WAGON          12356
Taxi                                    3482
Pick-up Truck                           2373
TAXI                                    1892
Box Truck                               1659
Bike                                    1190
Bus                                     1162
dtype: int64

Filling Unknow values with a placeholder

The top “cause” is an "Unspecified" placeholder. This is useful instead of a null value as it makes the distinction between a value that is missing because there were only a certain number of vehicles in the collision versus one that is because the contributing cause for a particular vehicle is unknown.

The vehicles columns don’t have an equivalent, but we can still use the same technique. Here’s the logic we’ll need to do for each pair of vehicle/cause columns:

• For values where the vehicle is null and the cause is non-null, set the vehicle to Unspecified.
• For values where the cause is null and the vehicle is not-null, set the cause to Unspecified.

def summarize_missing():
    v_missing_data = []

    for v in range(1,6):
        v_col = 'vehicle_{}'.format(v)
        c_col = 'cause_vehicle_{}'.format(v)

        v_missing = (mvc[v_col].isnull() & mvc[c_col].notnull()).sum()
        c_missing = (mvc[c_col].isnull() & mvc[v_col].notnull()).sum()

        v_missing_data.append([v, v_missing, c_missing])

    col_labels = columns=["vehicle_number", "vehicle_missing", "cause_missing"]
    return pd.DataFrame(v_missing_data, columns=col_labels)

summarize_missing()

	vehicle_number	vehicle_missing	cause_missing
0	1	204	24
1	2	3793	223
2	3	242	24
3	4	50	3
4	5	10	0

for v in range(1,6):
    v_col = 'vehicle_{}'.format(v)
    c_col = 'cause_vehicle_{}'.format(v)
    mvc[v_col] = mvc[v_col].mask( mvc[v_col].isnull() & mvc[c_col].notnull(), 'Unspecified')
    mvc[c_col] = mvc[c_col].mask(mvc[v_col].notnull() & mvc[c_col].isnull(), "Unspecified")

summarize_missing()

	vehicle_number	vehicle_missing	cause_missing
0	1	0	0
1	2	0	0
2	3	0	0
3	4	0	0
4	5	0	0

Missing data in the “location” column

Let’s view the work we’ve done across the past few screens by looking at the null correlation plot for the last 10 columns:

veh_cols = [c for c in mvc.columns if 'vehicle' in c]
plot_null_correlations(mvc[veh_cols])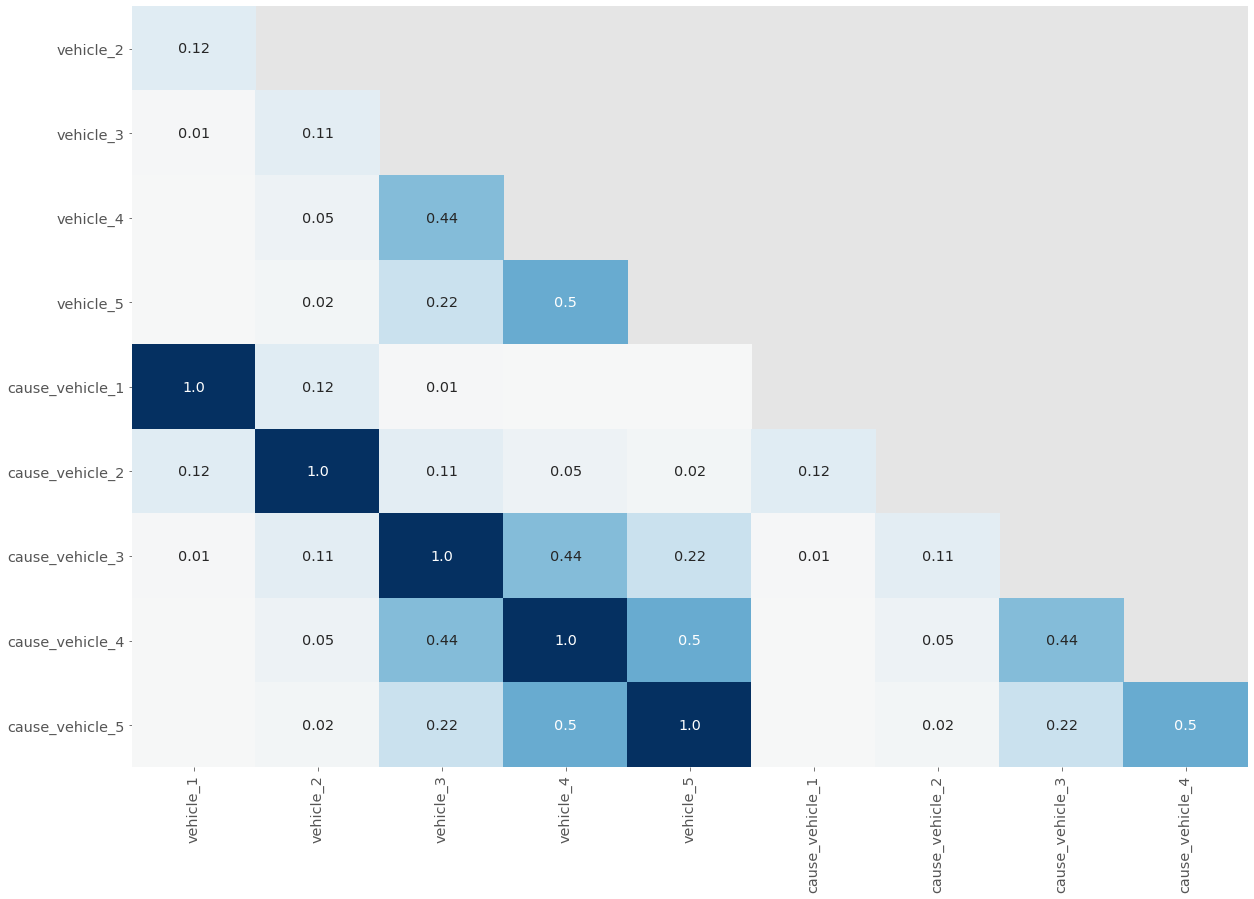

You can see the perfect correlation between each pair of vehicle/cause columns represented by 1.0 in each square, which means that there is a perfect relationship between the five pairs of vehicle/cause columns

Let’s now turn our focus to the final set of columns that contain missing values — the columns that relate to the location of the accident. We’ll start by looking at the first few rows to refamiliarize ourselves with the data:

loc_cols = ['borough', 'location', 'on_street', 'off_street', 'cross_street']
location_data = mvc[loc_cols]
location_data.head()

	borough	location	on_street	off_street	cross_street
0	MANHATTAN	(40.742832, -74.00771)	WEST 15 STREET	NaN	10 AVENUE
1	BROOKLYN	(40.623714, -73.99314)	16 AVENUE	NaN	62 STREET
2	NaN	(40.591755, -73.9083)	BELT PARKWAY	NaN	NaN
3	QUEENS	(40.73602, -73.87954)	GRAND AVENUE	NaN	VANLOON STREET
4	BRONX	(40.884727, -73.89945)	NaN	208 WEST 238 STREET	NaN

Next, let’s look at counts of the null values in each column:

location_data.isnull().sum()

borough         20646
location         3885
on_street       13961
off_street      44093
cross_street    29249
dtype: int64

These columns have a lot of missing values! Keep in mind that all of these five columns represent the same thing — the location of the collision. We can potentially use the non-null values to impute some of the null values.

To see where we might be able to do this, let’s look for correlations between the missing values:

plot_null_correlations(location_data)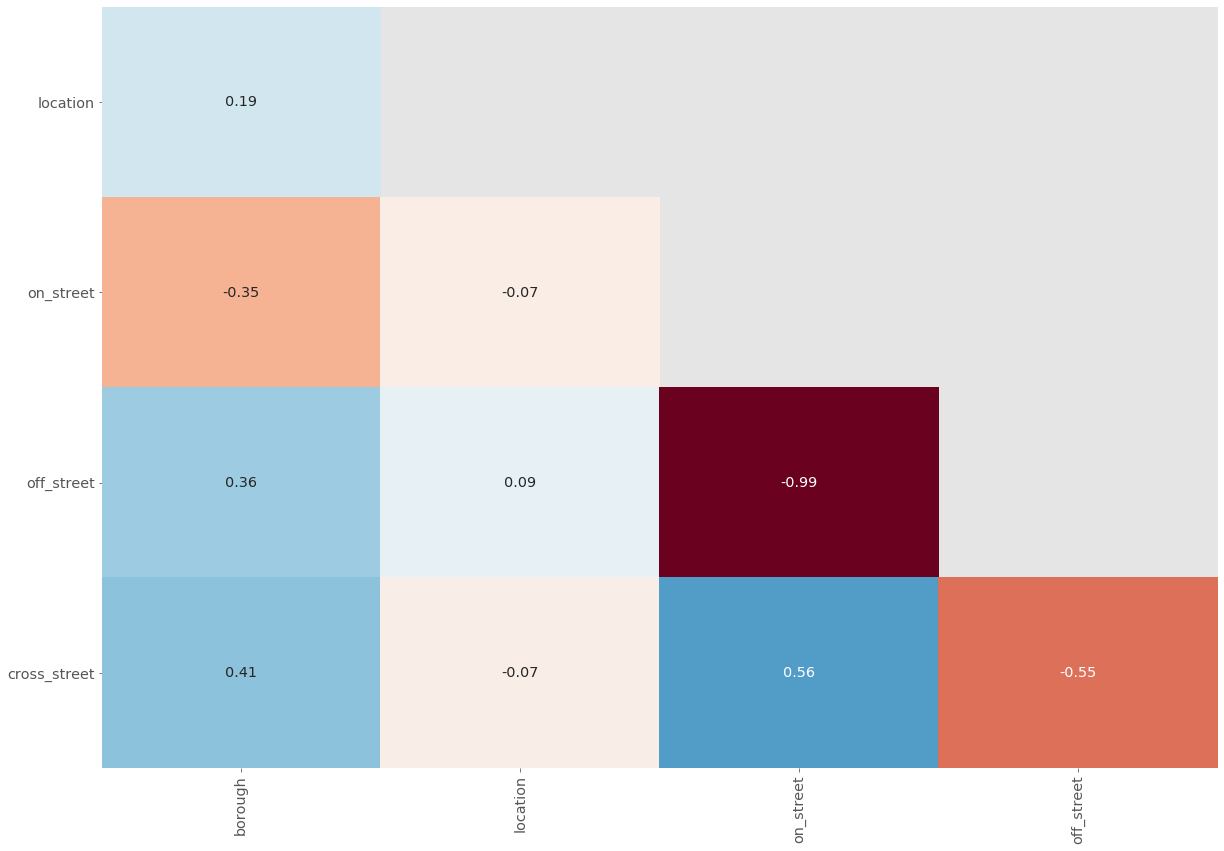

None of these columns have strong correlations except for off_street and on_street which have a near perfect negative correlation. That means for almost every row that has a null value in one column, the other has a non-null value and vice-versa.

The final way we’ll look at the null values in these columns is to plot a null matrix, but we’ll sort the data first. This will gather some of the null and non-null values together and make patterns more obvious:

sorted_location_data = location_data.sort_values(loc_cols)
plot_null_matrix(sorted_location_data)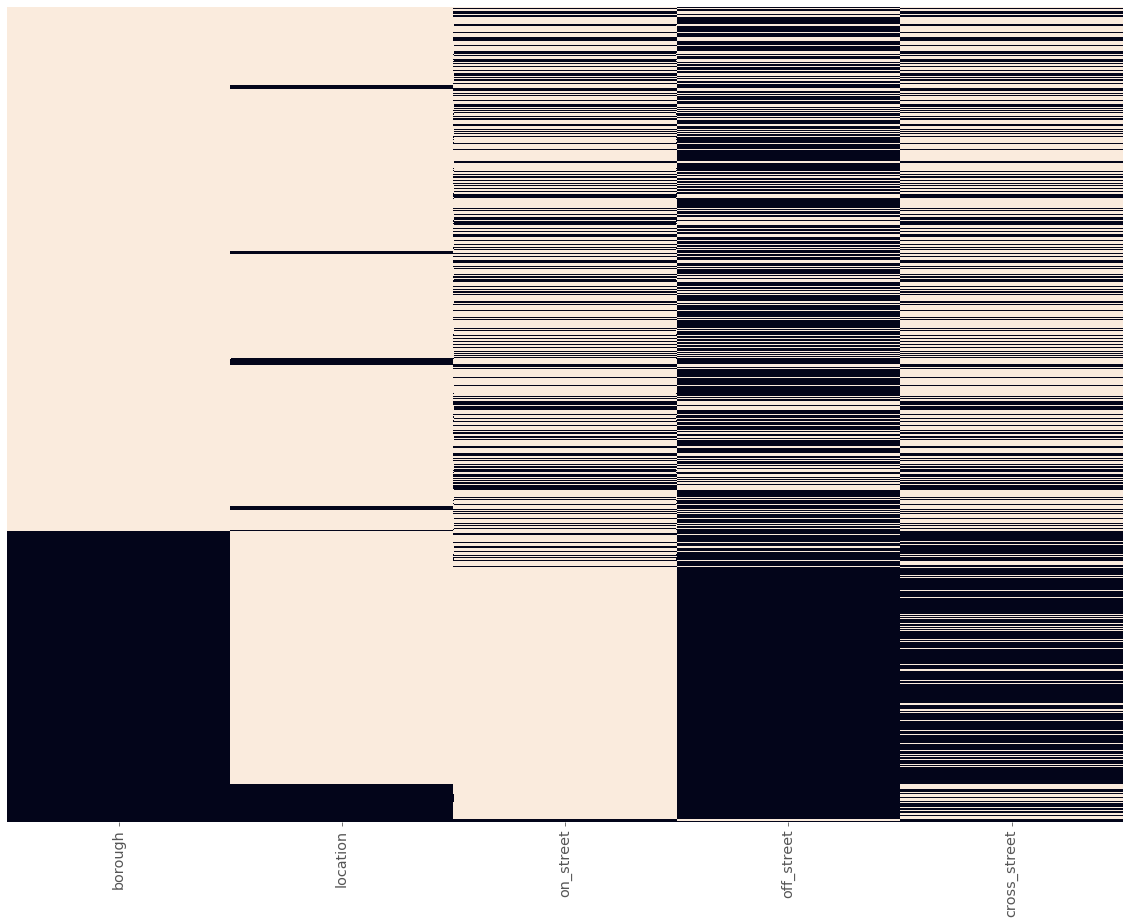

Let’s make some observations about the missing values across these columns:

• About two-thirds of rows have non-null values for borough, but of those values that are missing, most have non-null values for location and one or more of the street name columns.
• Less than one-tenth of rows have missing values in the location column, but most of these have non-null values in one or more of the street name columns.
• Most rows have a non-null value for either on_street or off_street, and some also have a value for cross_street.

Combined, this means that we will be able to impute a lot of the missing values by using the other columns in each row. To do this, we can use geolocation APIs that take either an address or location coordinates, and return information about that location.

Imputing Location Data

sup_data = pd.read_csv('../datasets/supplemental_data.csv')
sup_data.head()

	unique_key	location	on_street	off_street	borough
0	3869058	NaN	NaN	NaN	NaN
1	3847947	NaN	NaN	NaN	NaN
2	3914294	NaN	BELT PARKWAY	NaN	BROOKLYN
3	3915069	NaN	NaN	NaN	NaN
4	3923123	NaN	NaN	NaN	NaN

The supplemental data has five columns from our original data set — the unique_key that identifies each collision, and four of the five location columns. The cross_street column is not included because the geocoding APIs we used don’t include data on the nearest cross street to any single location.

Let’s take a look at a null matrix for the supplemental data:

plot_null_matrix(sup_data)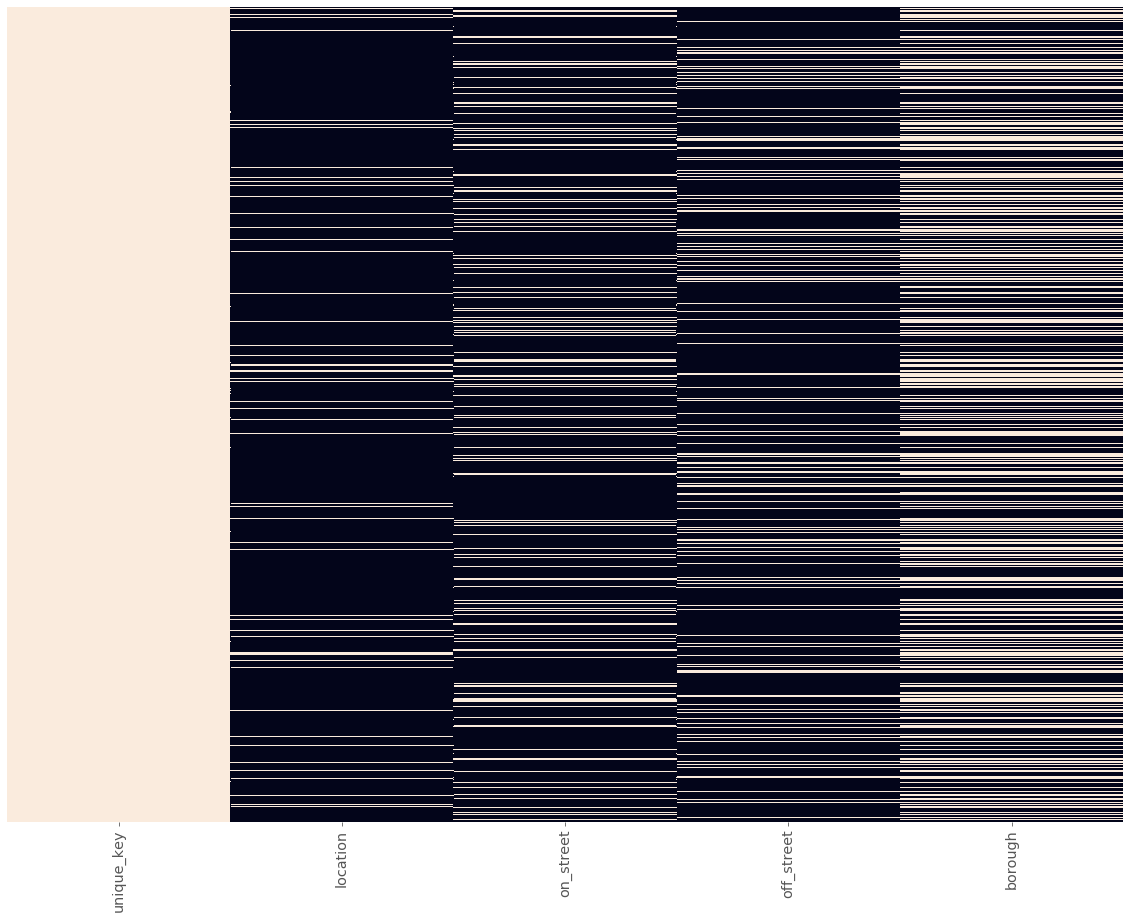

Apart from the unique_key column, you’ll notice that there are a lot more missing values than our main data set. This makes sense, as we didn’t prepare supplemental data where the original data set had non-null values.

mvc.unique_key.equals(sup_data.unique_key)

True

both the original and supplemental data has the same values in the same order, we’ll be able to use Series.mask() to add our supplemental data to our original data.

location_cols = ['location', 'on_street', 'off_street', 'borough']
mvc[location_cols].isnull().sum()

location       3885
on_street     13961
off_street    44093
borough       20646
dtype: int64

for c in location_cols:
    mvc[c] = mvc[c].mask(mvc[c].isnull(), sup_data[c])
    
mvc[location_cols].isnull().sum()

location         77
on_street     13734
off_street    36131
borough         232
dtype: int64

we’ve imputed thousands of values to reduce the number of missing values across our data set. Let’s look at a summary of the null values

mvc.isnull().sum()

unique_key                 0
date                       0
time                       0
borough                  232
location                  77
on_street              13734
cross_street           29249
off_street             36131
pedestrians_injured        0
cyclist_injured            0
motorist_injured           0
total_injured             21
pedestrians_killed         0
cyclist_killed             0
motorist_killed            0
total_killed               1
vehicle_1                151
vehicle_2               8469
vehicle_3              54110
vehicle_4              57108
vehicle_5              57671
cause_vehicle_1          151
cause_vehicle_2         8469
cause_vehicle_3        54110
cause_vehicle_4        57108
cause_vehicle_5        57671
dtype: int64

If we’d like to continue working with this data, we can:

• Drop the rows that had suspect values for injured and killed totals.
• Clean the values in the vehicle_1 through vehicle_5 columns by analyzing the different values and merging duplicates and near-duplicates.
• Analyze whether collisions are more likely in certain locations, at certain times, or for certain vehicle types.